分母に分数 280393-分母に分数がある計算

 この操作のことを「\(\dfrac{1}{4×5}\) を部分分数分解する」と言います。 微分や積分など、複雑な計算をするときは部分分数分解で「分数の足し算」に変形すると計算が楽になるケースが少なくありません。 部分分数分解をマスターすると、そういった複雑な計算でつまずく事がグッと分数は上 (分子)÷下 (分母)で表すことができます。 この考え方から 分母と分子が分数になったとしても このように計算できるというわけです。 この計算に慣れてきた人は、このように割り算部分を省略して 分母をひっくり返して、分子にかける と覚えておいても良いです。 分母を1にする数を分母、分子にかける 次は、分母を1にする数が掛けるという発想です。 分数は、分母と分子に同じ数をか 少し複雑に見えますが， 両辺の分母の形を頑張って覚えましょう。 1と2を覚えれば3も覚えられます。より一般的な形はヘビサイドの展開定理の定理1をどうぞ。 以下では，基本形をふまえて部分分数分解の方法（ a, b, c a,b,c a, b, c の求め方）を3通り解説します。 方法1：分母を

異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料

分母に分数がある計算

分母に分数がある計算-そして割り算は単純に計算したら小数になるということです。 1 ÷4＝025 1 ÷ 4 ＝ 025 つまり、分数を小数に治す方法は、『分数→割り算』と変換して計算すればいいだけなのです。 ただし分数の中でも小数で表せないものは数多くあります。 1 3 ＝1 ÷3＝0 分母 denominator 数学の分数には、分子と分母が含まれます。 Fractions in math include a numerator and a denominator 数学では、分母は分数の一番下の数です。 In mathematics, the denominator is the bottom number in fractions 数学では、分母はアイテムが分割される等しい部分の数を表し

分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋

分母は、分数式の横線の下側（右側）にくる数です。 割り算でいう、「割る数」が分母です。 分数の意味、分子との関係など復習しましょう。 上側（左側）にくる数を分子といいます。 下記も参考にしてくださいね。 分数とは？ 1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方 数学の分子とは？ 1分でわかる意味、分母、0との関係、分母と分子を入れ替える計算 管理人おすすめ！分母に分数を含む式 ここでは、分母に分数を含む式の計算のしかたについてみていきましょう。 次の式を簡単にしなさい 難しい分数式を考える前に、簡単な分数を例に考えてみましょう。 この分数式について考えてみます。 おわりに ここでは、分母に三角関数が含まれているときの、不定積分の置換積分について見てきました。分母・分子に何かを掛けて変形するのは、難易度が高いですね。 $\cos x dx$ や $\sin x dx$ を生み出せないか、という発想で考えてみましょう。

 分数の計算方法を一覧にまとめました。 計算のやり方を忘れてしまったときには、こちらで確認しましょう。 分数の計算のやり方 分数の足し算のやり方 ①分母をそろえる ②分子どうしを足す ③約分する 〈分母が同じ分数の足し算〉 〈分母が違う分数の足し算〉 分数の引き算のやり方 意外に難しい問題ですよ。 ある分数が a/b と書けたならば、 a を分子、b を分母と考えることはできます。 しかし、 与えられた分数を a/b と表す a,b の組は、 一通りには決まりません。 例えば、2/5 を a/b と表す a,b は、 2,5 の他に、4,10 でも 06,15 でも 式中に分数が入る場合、因数分解をするために、まずは分数をなくす計算をしなくてなりません。 そのためには、まず分母に注目することから始めましょう。 分数をなくすことができれば、あとはいつもどおりの因数分解ができます。 目次 1 分数が

 この分数の分母を払うとき 分母に注目すると、 (1iz)(1iz)となってるのですがかけたzって共役な複素数じゃないんですか？ 数学 誘電率の複素数の意味がわかりません。 あなたは部分分数分解を単なる「式の変形」だと思い込んでいませんか？ 実は数学b の数列の単元や数学3の積分計算でとてもお世話になる、大切な式変形なんです。 今回は、その「部分分数分解」を、公式・やり方だけでなく数列の問題への応用を詳しく解説しました!実は、\( 2k1\) と \( 2k1\) の差が 2 なので分母に2を持ってくれば良いのですが、因数が3つなどになると違った方法になりますので、覚えておくより通分してその都度求めた方が確実です。 では、部分分数に変形できたとして計算をしてみましょう。

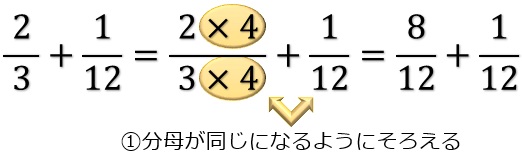
分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ

分母にxのある方程式の解き方を教えて頂けますか 分母にxのある方程 数学 教えて Goo

(A) 一般に，分数関数は（分子）÷（分母）の割り算によって商と余りに分けると，「 分子の次数＜分母の次数の形 」 （数研の参考書で「分数式は富士の山」と呼ばれるもの） に変形することができる．この変形により，分数関数の不定積分を求めるときは，分子の次数が分母の次数よりも低い形だけを考えればよいことになる． (B) また，分母が何次式であっても分母=0のn次方程式は1次式と2次式帯分数を入力する場合は、整数部分を入力してから、「と」ボタンで分母を入力、分母入力後に「分」ボタンで分子を入力。 上側スクリーンが帯分数表示、下側スクリーンが仮分数表示です。 分母を0にすることはできません。 0で割るとエラーになります。 分母に分数を含む分数式の計算方法を知りたい 次の式の計算をせよ。 「この計算方法を教えて下さい。 」という質問をいただきました。 では、実際に計算していってみましょう！ ！ まず、分母の を計算してみましょう。 となります。 となります。

分母がマイナスの時の分数の扱い 数学の基本 Youtube

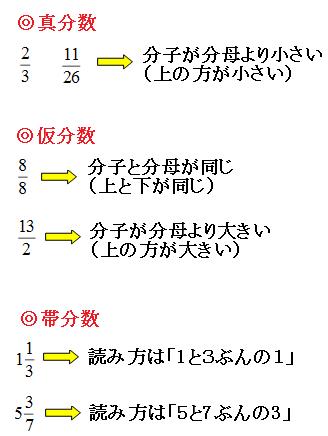
分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利

分母にマイナスついている場合もありますよ!分子にもマイナスがつく場合もあります。 例を挙げて説明すると、 (3/4)=3÷4=3÷（4) となり、結果的に計算結果は変わらないため、どちらにつけても間違いではないです。 ただ、やはり答えとしてきれいなのは線の真ん中にマイナスがつくものです。 分数関数の積分は、式の形によって解き方を工夫する必要があります。 代表的なパターンを確認していきましょう。 ① 分子に分母の微分が隠れているパターン 分子に分母の微分の形があれば、次の積分公式を利用できます。このように考えていけば、分母が何個の積だってみな部分分数分解が可能になってしまう。では、 なんかは、どう分解されるだろうか。 ＜まなぶ＞ はい、nとn3の部分で分解します。 となります。 ＜先 生＞ 素晴らしい。

分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学

Printablesは 一般的な分母で分数を引く練習をします

つまり、 となることはないので、分母分子を で割ってOKです。 ここまできたら簡単だ。 分かります。 分母の は相加相乗平均より だから、 今回分子は1の定数で、分母は3以上。 分母分子ともに正で分子が定数のときは、分母の値が大きくなればなるほど分数全体の値としては逆に小さくなる。 だから となる。 だから、今回の分数 の最大値は となります！ ！ (＊ は大なりイコール（以上）のこと分数式は， 分子を分母で割って商と余りを計算する ことで，「多項式」＋「分子の方が次数が低い分数式」に変形できます。 →多項式の割り算の二通りの計算方法と例題 例 x 2 3 x 5 x 1 \dfrac {x^23x5} {x1} x 1x2 3x 5 に対して，分子を分母で割ると x分数のなかに分数が含まれる計算の解説プリント 分数の中に分数が含まれる計算の解説 分数の中に分数が含まれるものの解法については主に2種類あります。 まず、ひとつめの割り算を使う解法です。 \(\frac{b}{a}=b\div a\)なんだよね。

分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋

分数の方程式の解き方 分母を消せば中１の子でも絶対解ける 中学や高校の数学の計算問題

分数をパーセントに直す具体例 例題 (1) 3 4 をパーセントに直せ。 (2) 2 7 をパーセントに直せ。 解答 (1) 分子÷分母×100 = 3 ÷ 4 × 100 = 075 × 100 = 75 75 ％ (2) 分子÷分母×100 = 2 ÷ 7 × 100 = ⋯ × 100 = ⋯ 約 286 ％ 例題 (2) のように、割り算がいつまでも終わらずに続くこともあります。 関連： 分数を小数に直す方法と例題 補足、まめ知識 ・逆に、パーセントを分数 分数の分母・分子ともに小数であっても構いませんよ． > 分母が整数、分子が整数＋少数 という事は，例えば ()/1234 みたいな分数ですね． これは紛れも無い分数です．但し，できるだけ簡単な分数にした方がいいですね． 例えば， ()/1234 という分数であれば， ()/1234 =1234/1234 =1/10 と既約分数（それ以上約分できない形の分数）にする事が望ま分数の方程式は、とにかく 分母をはらう！ というのがポイントとなります。 それは分母に があっても同じこと こうすることによって、方程式を普通の形に変形することができます！ それでは、このやり方で方程式を解いていきましょう。 両辺に を掛けると 両辺に を掛けると 両辺に を掛けると 両辺に を掛けると まとめ とにかく分母をはらう！ これが大事ですね。 高校数学になると、このような

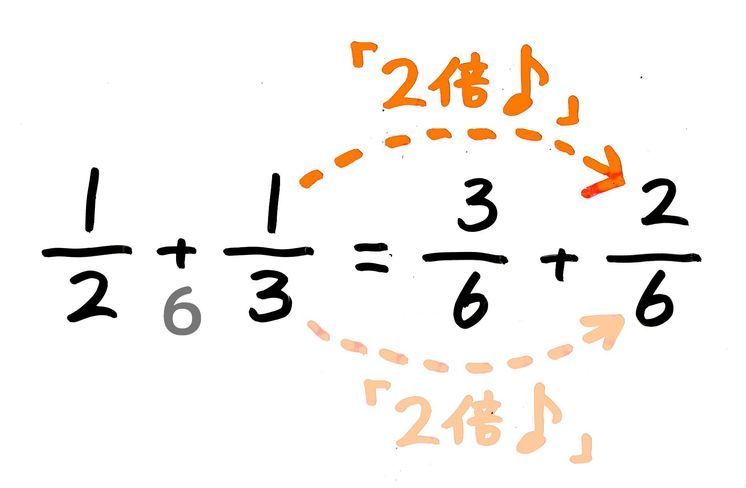
小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館

数学 分数の中に分数がある場合の計算の方法

分母に分数を含む分数式 分母に分数がある場合の分数式の計算方法をみてみましょう。 ① こんな場合です。うーん、どうやってとけばいいでしょうか。 そもそも分数とは でしたね。①の式を 割り算の形に変形してみましょう。分母と分子に同じ数をかけて、同じ大きさの分数を作る学習プリントです。 分母と分子を何倍ずつするのかを見極める問題と、2倍・3倍として分数を作っていく問題です。（例：4/7 = 8/14 = 12/21）『すらぷり』は無料で使える学習プリントです！ 分数式とは まずはじめに、分数式とは 分母、分子に文字が入っている分数 のことだと思えばよいです。分数式は基本的に普通の分数と同じで 一番簡単な形になるまで変形しなくてはいけません 。 ここではその分数式を計算する方針と方法を説明します。

3

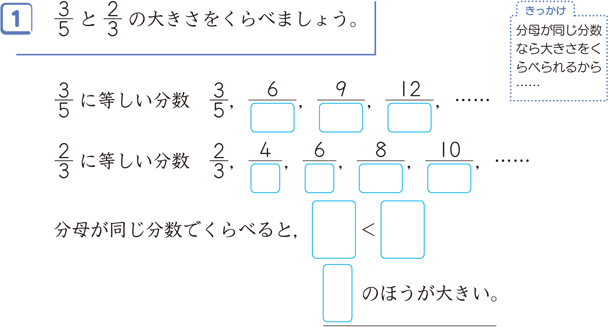
通分と約分 算数用語集

分母が3次の部分分数分解 公式 分母が3次の部分分数分解の公式は以下の通りです。 分子の最大次数は2次になります。 分母が3次の部分分数分解としては4種類の分解方法があります。分母が2次の部分分数分解で説明したように、 分子の形に注目する必要はこの公式について理解するコツは、分母が関数の分数を、以下の通り、1 を指数とする べき乗 ・・・ に置き換えることにあります。 なお、べき乗関数の微分については『 べき乗（累乗）の微分公式誰でも必ず深く理解できるように解説 』で解説してい 分母と分子に同じ数をかけても分数の値自体に変化はない ・・・ので001を整数にすべく分母・分子に100をかけると・・・100/1 = 100 0

３年算数分数のたし算ひき算 わかる教え方

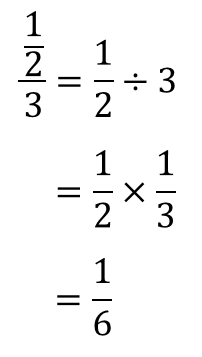
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

分数には、「 分母と分子に同じ数をかけ算しても、同じ数でわり算しても、大きさは変わらない 」という性質があります。 特に、 分母と分子を同じ数でわり算して、なるべく小さな数にすることを約分 といいます。 分数はできるだけ約分をするのがマナーです。 分数が出てきたら、いつでも「約分できるかな？ 」って考えるようにしましょう。 （例題4） 次の分数を約分しましょう。 分母と分子

三年级数学上册同分母分数的加减法口算题卡 给孩子练练 分子

分数関数の不定積分

異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料

分数の引き算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス

分数の掛け算の上手な教え方 なぜ分母同士 分子同士をかけるのか 数学fun

分母の数が大きい場合の計算 連立方程式 中学生からの勉強質問 数学 進研ゼミ中学講座

算数4年から6年

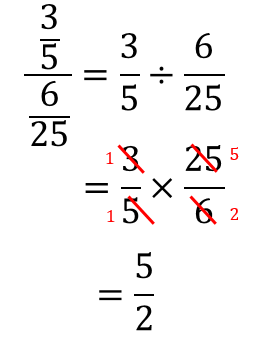
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

分数とは 大人の学び直し算数 計算のやり方解説 無料

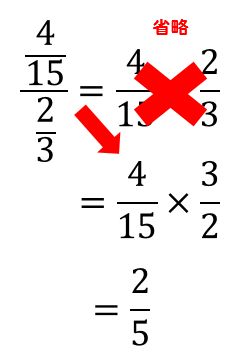
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

半分数 分数の解き方がわかりません 半分数の分母の分数の分母を消したいの Yahoo 知恵袋

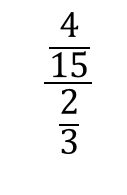
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

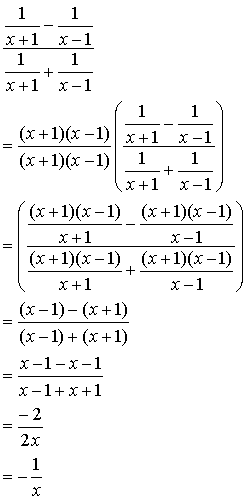
分数の復習と分数式の計算

分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題

繁分数式の解き方について この 分母と分数にかけてとくー というのは Yahoo 知恵袋

数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo

分数の通分の意味とやり方 子どもに教える際のポイントやコツを解説 数学fun

高校数学 繁分数式 分数の分数 の計算 受験の月

単項式の乗除 分数の割り算の問題は 分子と分母の分け方に注目 中学や高校の数学の計算問題

分母に Xがある 方程式の解き方について 40 4 1 X が なぜ X 40 に 高校 教えて Goo

分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ

分数 分数の方程式をいじってみよう 15 Do Your Best Haruka Saki

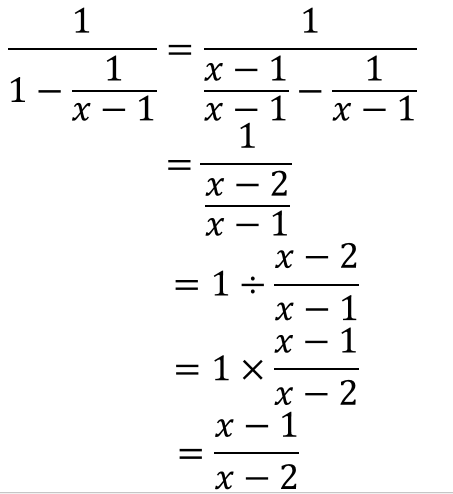
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

小学４年生の算数 同じ分母の分数のたし算 練習問題プリント ちびむすドリル 小学生

小学5年生 算数 無料問題集 分母が違う帯分数の足し算 おかわりドリル

異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料

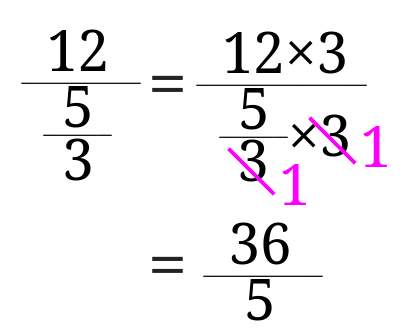
分数の中に分数のような繁分数の計算の仕方がわからない さびねこ中学校

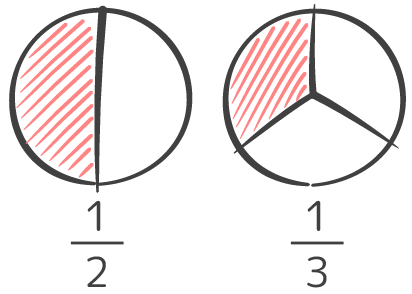
小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館

分数の割り算の計算方法 どうして分子と分母を入れ替えて掛け算する

数 式と計算 分数の中に分数 繁分数 オンライン無料塾 ターンナップ Youtube

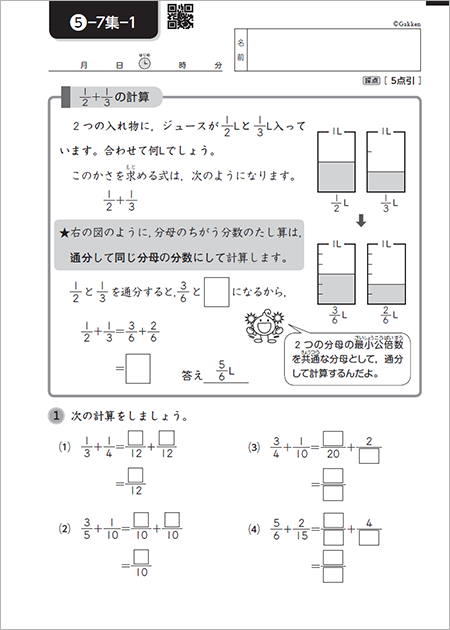
学研教室

Core Ac Uk

分数の通分 分母と分子に同じ数をかける 小5算数 無料プリント

分数の掛け算は なぜ分母同士 分子同士を書けるの 元小学校教師が教える できる子ども育成塾 小岩 個別指導塾 小学生専門 国語と算数の苦手を克服

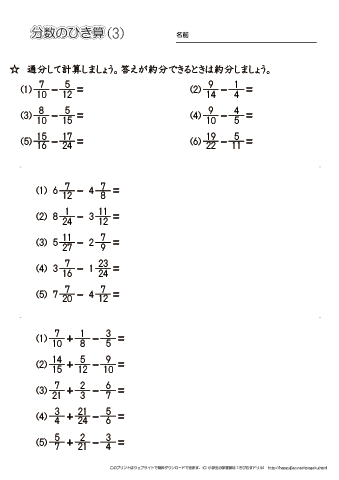
小学５年生の算数 異分母の分数の引き算 問題プリント ちびむすドリル 小学生

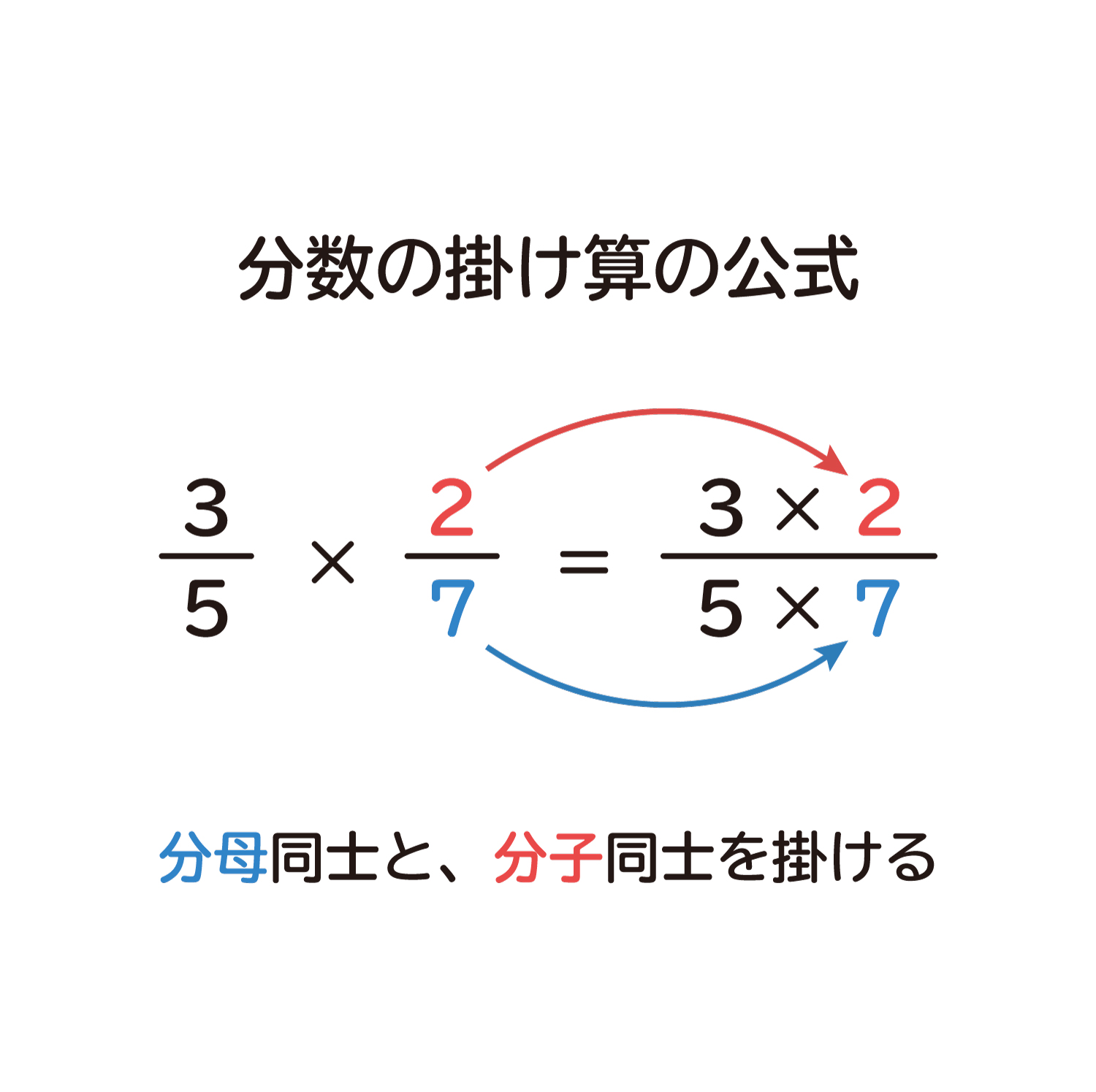
なぜ 分数の掛け算は分母同士 分子同士を掛ける のか を説明します おかわりドリル

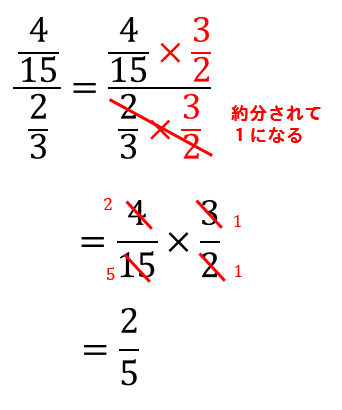
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

分母が違う分数の足し算 通分して計算する理由は分配法則を考えればわかる 数学の面白いこと 役に立つことをまとめたサイト

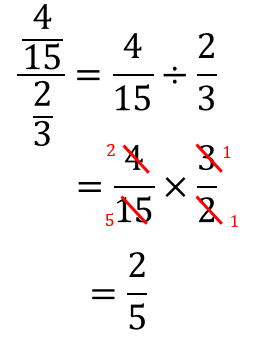
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

分数の引き算の計算プリント 分母が異なる問題 全240問無料 算数パラダイス

分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun

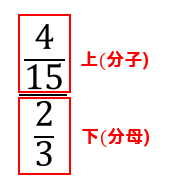
分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

1

分数の掛け算は なぜ分母同士 分子同士を書けるの 元小学校教師が教える できる子ども育成塾 小岩 個別指導塾 小学生専門 国語と算数の苦手を克服

三年级数学上册同分母分数的加减法口算题卡 给孩子练练 分子

分数のわり算２ 分母どうし分子どうし割ってはいけないか

分母が同じ数字の掛け算についての質問です 今更ながら十年近くぶ Yahoo 知恵袋

異分母の足し算のやり方 大人の学び直し算数 計算のやり方解説 無料

经典 异分母分数加减法练习题 松鼠文库

1

分数の足し算の計算プリント 分母が異なる問題 全２４０問無料 算数パラダイス

三年级数学 分数 异分母分数加法 Youtube

小学５年生の算数 異分母の分数の足し算 練習問題プリント ちびむすドリル 小学生

分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

数学 分数の中に分数がある場合の計算の方法

なぜ分母に分数を代入するのこうなるのですか たまたま元の式に似た形 Yahoo 知恵袋

24 异分母分数加减混合运算 Youtube

方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題

分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ

分数分の分数の計算にルートが入った計算がさっぱりわかりません Yahoo 知恵袋

みんなの算数オンライン 教科書 分母の異なる分数の足し算

小学5年生 算数 無料問題集 分母が違う分数の足し算 おかわりドリル

数学の問題なのですがなぜ分数の分母を残すか残さないかの判断が分 Yahoo 知恵袋

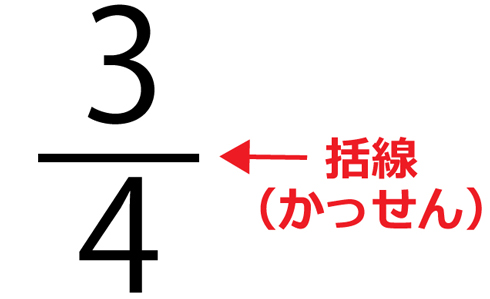
分数に使われる あの横線 の名前 知ってる ねとらぼ

分数の足し算 分母が同じ 答えが1以上 計算ドリル 問題集 数学fun

秋篠理数 算数教室の さあさあ お勉強だよ

分数とは 大人の学び直し算数 計算のやり方解説 無料

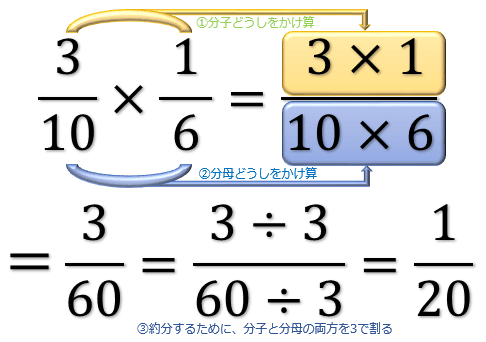
分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ

通分と約分 算数用語集

数学 分母が3次までの部分分数分解の公式 全６パターンの解法紹介

分母が分数とはどういうことでしょうか 二分の一の分母は Yahoo 知恵袋

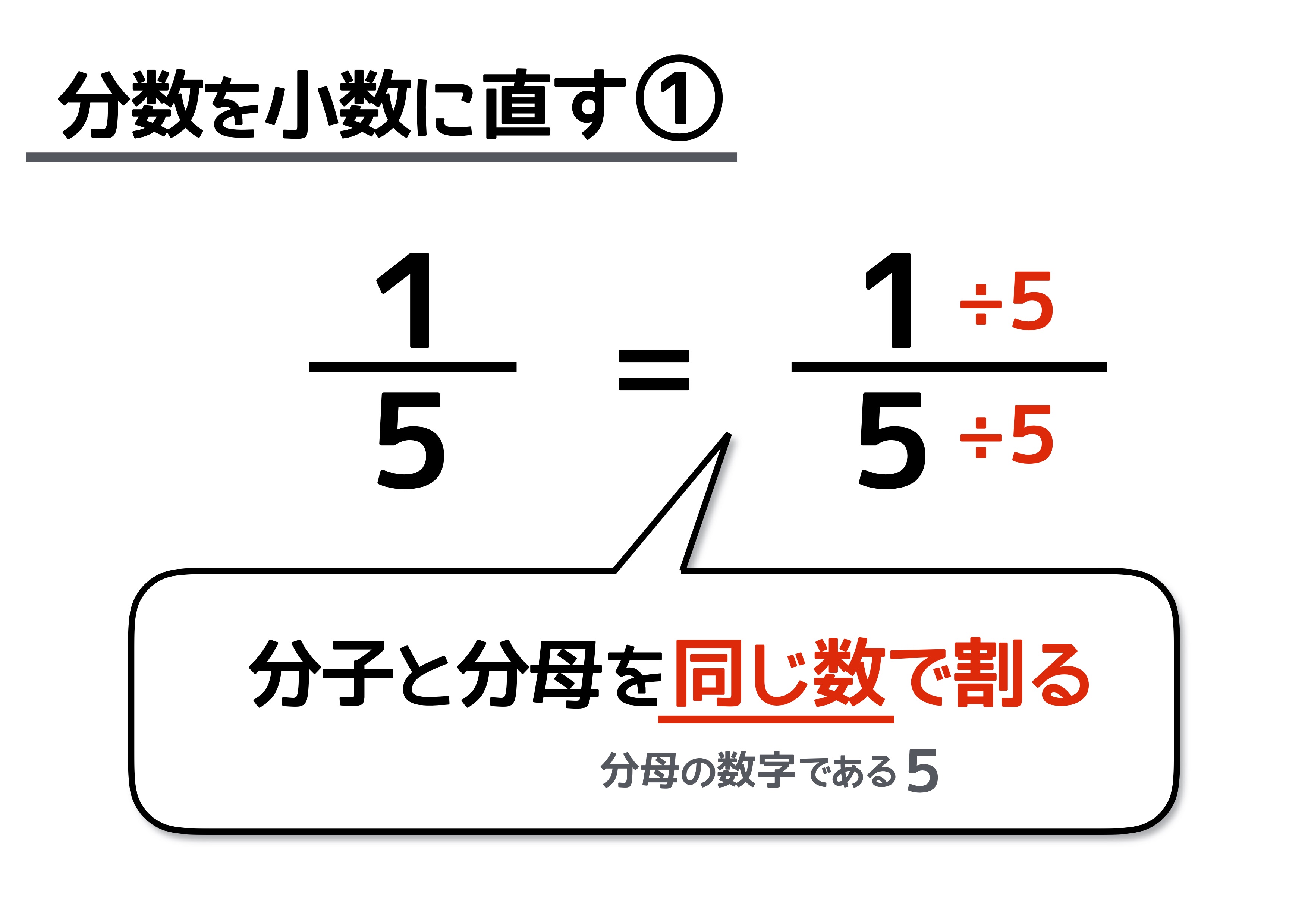
分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ

小学生向け 算数 プリント 分母が同じ分数同士の足し算 学習塾 Step By Step

数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo

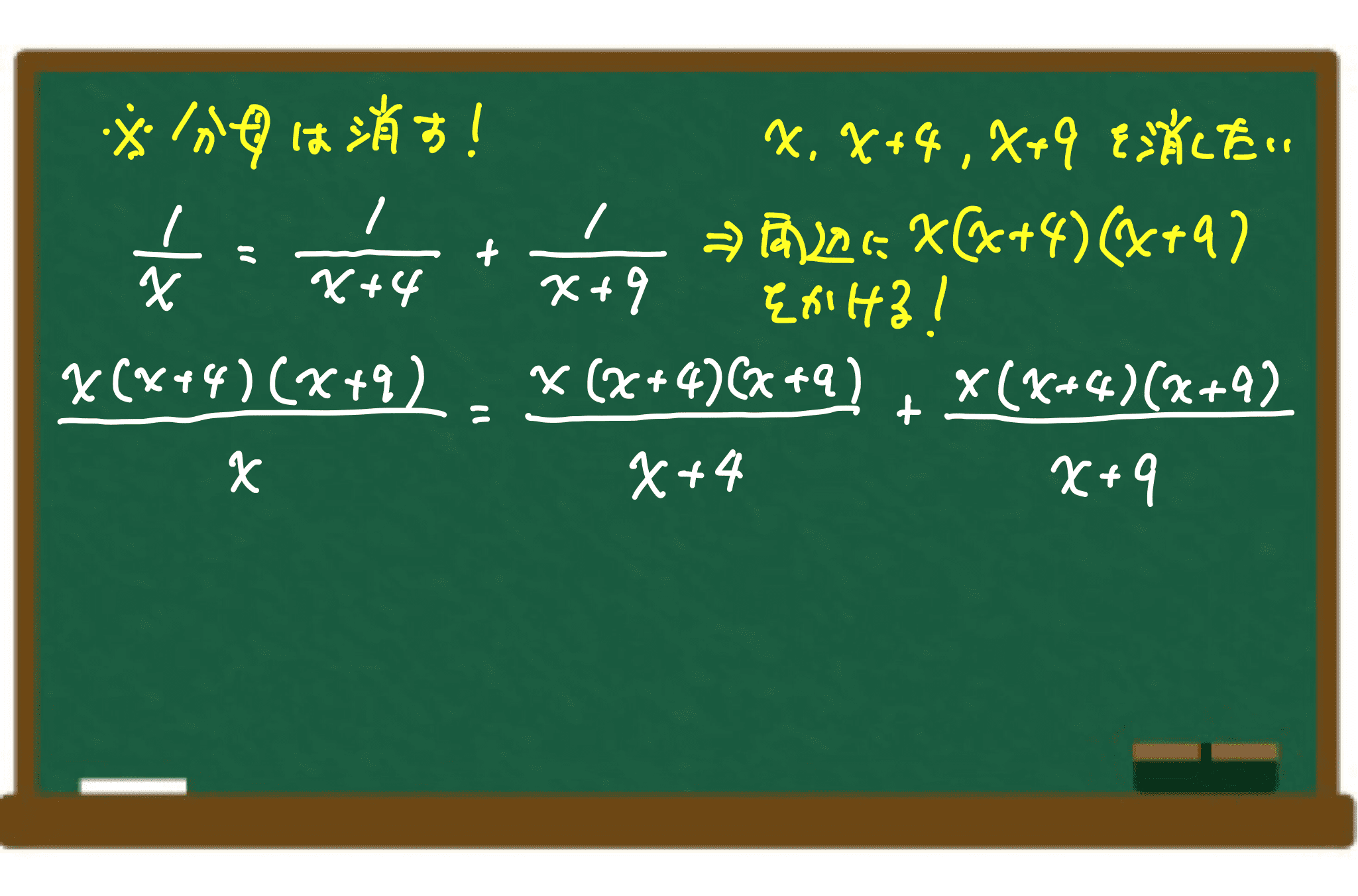
分数の計算 公務員試験のプロが独学受験生を応援するブログ

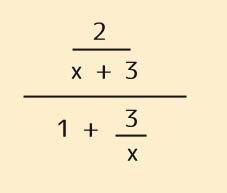
英語で分数の読み方と表現 何分の1 はどう言う 分子 分母は 話す英語 暮らす英語

分母をたす 間違いを防ぐ 分数たし算をイメージと色で描く 図式

すごく初歩的なことがわからなくなってしまいました 分数の分母を消す方法です Clearnote

1

異分母の引き算のやり方 大人の学び直し算数 計算のやり方解説 無料

分母 分子にまた分数が含まれる 繁分数 15 Do Your Best Haruka Saki

分母を払うというやり方がよく分かりません 詳しく説明して頂けませんか 分 Yahoo 知恵袋

小学3年生 算数 無料問題集 分母が同じ分数の足し算 おかわりドリル

帯分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス

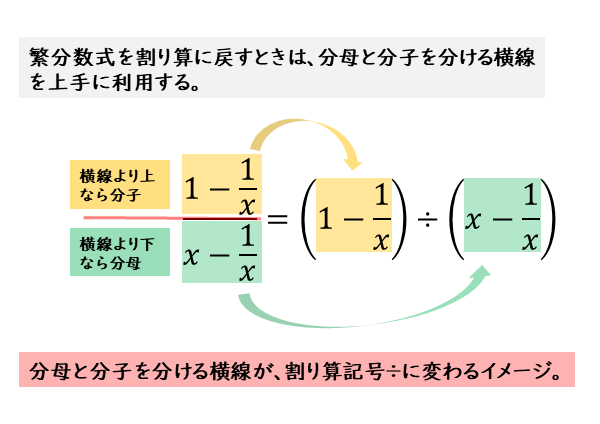
式と証明 繁分数式の計算について 日々是鍛錬 ひびこれたんれん

分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ

分数の引き算 分母が異なる 計算ドリル 問題集 数学fun

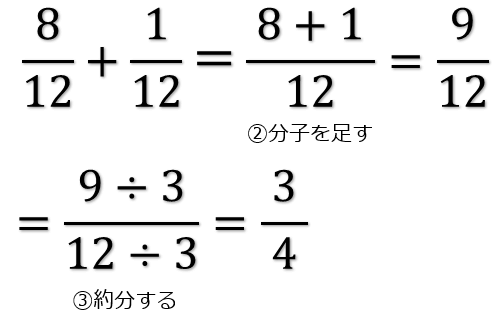
分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ

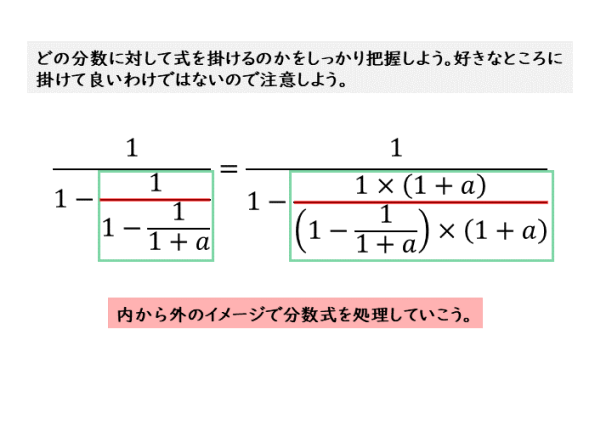
式と証明 繁分数式の計算について 日々是鍛錬 ひびこれたんれん

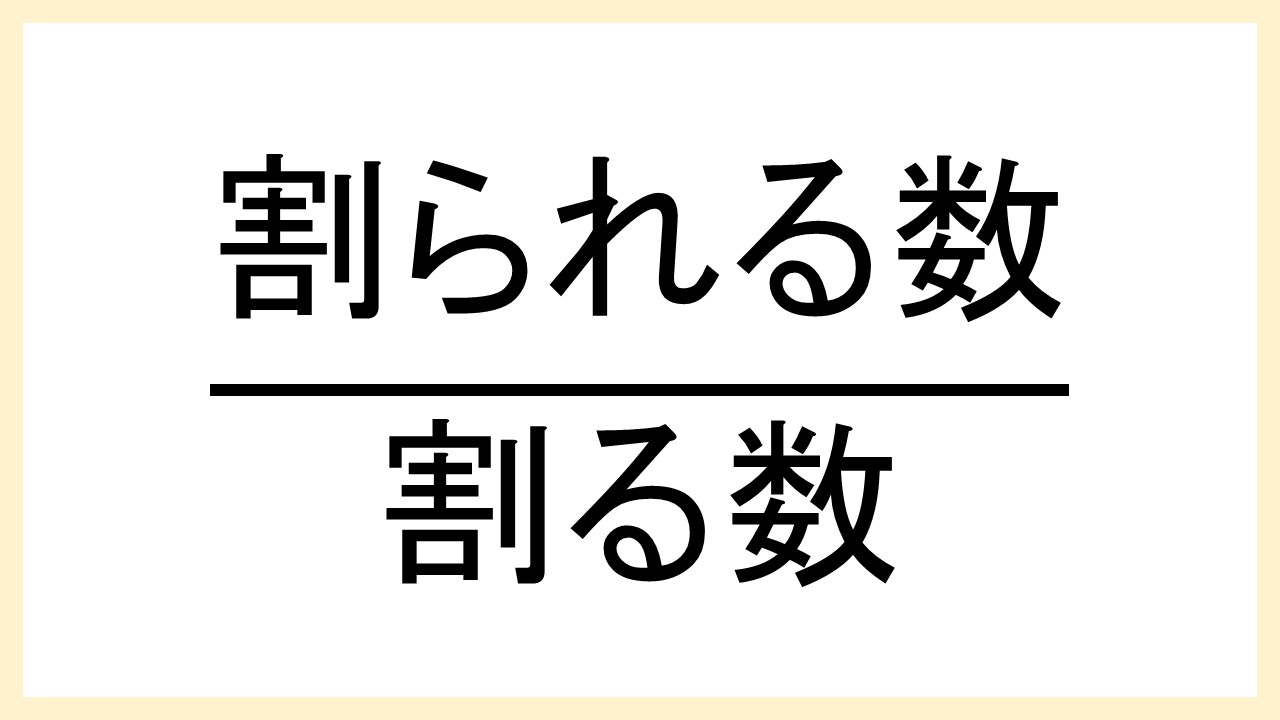
よくわかる 分数を割り算に直す方法 例題あり

Incoming Term: 分母に分数を含む分数式の計算, 分母に分数, 分母に分数の計算, 分母に分数 解き方, 分母に分数がある計算, 分母に分数の足し算, 分母に分数があるときの計算,